
내용 참고
Microsoft Docs (구 MSDN)
영문 wikipedia
나무위키
C언어 이론 11 / 그 외 기본 타입들 (2)
■ 이번 포스트에서는 정수형과 실수형을 제외한 char, bool, void 타입에 대해서 다룬다.
Ⅱ. 논리형
ⅰ. 유래
■ 프로그램 언어의 bool 타입은 수학의 불 대수에서 유래된 타입이다.
■ 불 대수는 19세기 중반의 수학자 조지 불(George Boole)이 고안하고 형식화한 대수 체계이다.
■ 불 대수는 논리 연산이라고도 불리며, 참(1,true)과 거짓(0,false)의 두 개의 값에 대한 연산체계이다.
ⅱ. C언어
■ C99이전의 C언어는 기본 자료형으로 bool형을 제공하지 않으며 거짓을 0으로 참을 0이외의 모든 숫자(기본적으로 1)로 표시한다.
■ 0이외의 모든 숫자는 기본적으로 참을 의미하기에 -1이나 0.1 등의 수도 참을 의미함에 주의해야한다.
■ &&등의 논리 연산자나 if등의 조건 검사문은 결과가 거짓이면 0을, 참이면 1을 반환한다.
■ C99부터는 _Bool이라는 타입이 추가되었다.
■ 하지만 값으로 true,false가 아닌 값을 저장하며 0을 입력하면 내부적으로 0, 0이외의 값은 1로 저장한다.
■ C99에서는 이로 인한 혼란을 해결하기 위해서인지 stdbool.h라는 헤더파일에 true와 false를 매크로로 정의해놓고 있다.
■ stdbool.h 헤더파일에는 _Bool 타입은 bool로, true는 1, false는 0으로 정의되어 있다.
■ 즉 stdbool.h 헤더파일을 사용한다고 해서 bool형에 참을 0.1로 저장하는 것이 막히는 것은 아니니 주의할 필요가 있다.
ⅲ. C++
■ C++에는 기본자료형으로 bool 타입과 true, false값이 존재한다.
■ 즉, stdbool.h 헤더파일이 없어도 bool 타입과 true, false값을 쓸 수 있다.
■ 그 외에는 위의 C언어 항목에서 설명한 것과 동일하다.
Ⅲ. 논리연산
ⅰ. 수체계
■ 0(=false), 1(=true)
ⅱ. 연산의 종류
■ 한글 연산명, (영어 연산명, 일반적으로 사용되는 기호, C언어에서 사용되는 연산자) [C언어의 연산자 우선순위]의 순서로 표시했다.
■ 부정 (NOT; ¬; C::!) [3] : ¬0 = 1, ¬1 = 0
■ 논리합 (OR; ∨, C::|) [12] : 0∨0 = 0, 0∨1 = 1, 1∨0 = 1, 1∨1 = 1. (교환법칙이 성립한다.)
■ 부정 논리합 (NOR; ↓) : 0↓0 = 1, 0↓1 = 0, 1↓0 = 0, 1↓1 = 0. (¬(a∨b)와 같다.)
■ 배타적 논리합 (XOR; ⊕, C::^) [11] : 0⊕0 = 0, 0⊕1 = 1, 1⊕0 = 1, 1⊕1 = 0. (둘 중 하나만 참이어야 참.)
■ 논리곱 (AND; ∧, C::&) [10] : 0∧0 = 0, 0∧1 = 0, 1∧0 = 0, 1∧1 = 1. (교환법칙이 성립한다.)
■ 부정 논리곱 (NAND; ↑) : 0↑0 = 1, 0↑1 = 1, 1↑0 = 1, 1↑1 = 0. (¬(a∧b)와 같다.)
■ 배타적 논리곱 (XAND; ⊗, C::==) [9] : 0⊗0 = 0, 0⊗0 = 0, 0⊗0 = 0, 0⊗0 = 0. (¬(a⊕b)와 같다.)
■ 배타적 논리곱은 동치(EQV; =)라고도 부른다.
ⅲ. 주의사항 및 성질
■ 부울 대수에서는 참과 거짓만 존재하기 때문에 1∨1은 10이 아니다.
■ 이중부정(Involution) 법칙 : ¬(¬A)=A
■ 항등원(Identity) : A∨0 = A = 0∨A (논리합), A∧1 = A = 1∧A (논리곱)
■ 동일(Idempotent) 법칙 : A∨A = A (논리합), A∧A = A (논리곱)
■ 드모르간(DeMorgan) 법칙 : ¬(A∧B)=(¬A)∨(¬B), ¬(A∨B)=(¬A)∧(¬B)
■ 교환(Commutative) 법칙 : A∨B = B∨A (논리합), A∧B = B∧A (논리곱), A⊕B = B⊕A (배타적 논리합)
■ 위의 교환법칙에 따라 각 결과값에 부정을 취한 연산 (부정 논리합, 부정 논리곱, 배타적 논리곱)도 교환법칙이 성립한다.
■ 결합(Associative) 법칙 : (A∨B)∨C = A∨(B∨C) (논리합), (A∧B)∧C = A∧(B∧C) (논리곱), (A⊕B)⊕C = A⊕(B⊕C) (배타적 논리합)
■ 각 연산의 부정 연산에 대한 결합법칙은 성립하지 않는다.
■ 분배(Distributive) 법칙 : A∧(B∨C) = (A∧B)∨(A∧C), A∨(B∧C) = (A∨B)∧(A∨C), A∧(B⊕C) = (A∧B)⊕(A∧C)
■ 흡수(Absorption) 법칙 : A∨(A∧B) = A, A∧(A∨B) = A
■ 합의(Consensus) 법칙 : (A∧B)∨(B∧C)∨(C∧¬A) = (A∧B)∨(C∧(¬A)), (A∨B)∧(B∨C)∧(C∨¬A) = (A∨B)∧(C∨¬A)
■ 그 밖의 법칙 1 : A∨(¬A) = 1, A∧(¬A) = 0 / A+1=1, A∧0=0 / ¬(A⊕B) = A⊕(¬B) = (¬A)⊕B
■ 그 밖의 법칙 2 : (¬A)⊕(¬B) = A⊕B / A∨((¬A)∧B)=A∨B, A∧((¬A)+B)=A∧B
ⅳ. 몇몇 연산 법칙에 대한 증명
■ 항드원과 동일법칙에 대한 진리표를 이용한 증명

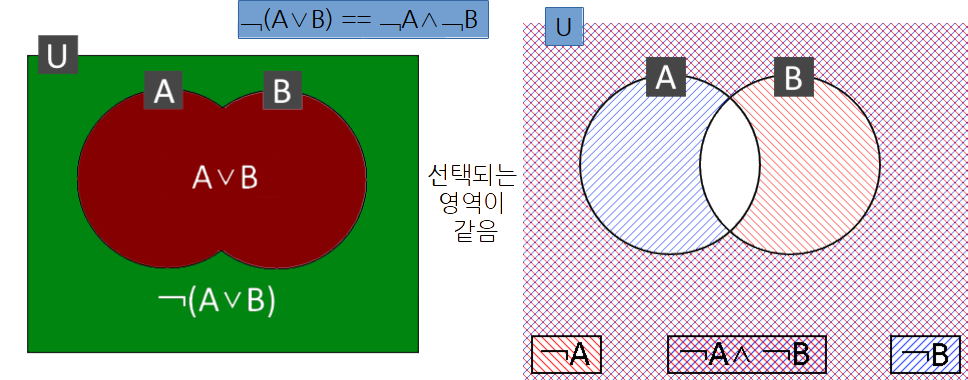
■ 드모르간 법칙에 대한 벤 다이어그램을 이용한 증명
■ 부정연산에 대한 결합법칙이 성립하지 않는다는 것에 대한 수식을 이용한 증명
→ (A↓B)↓C = ¬(A∨B)↓C = ¬(¬(A∨B)∨C) = ¬(¬(A∨B))∧¬C = (A∨B)∧¬C
→ A↓(B↓C) = A↓(¬(B∨C)) = ¬(A∨(¬(B∨C))) = ¬A∧¬(¬(B∨C)) = ¬A∧(B∨C)
→ A = 1, C = 0 일때 두 수식의 결과값이 다르므로 (A∨B)∧¬C ≠ ¬A∧(B∨C) ∴ (A↓B)↓C ≠ A↓(B↓C)