UpWrite

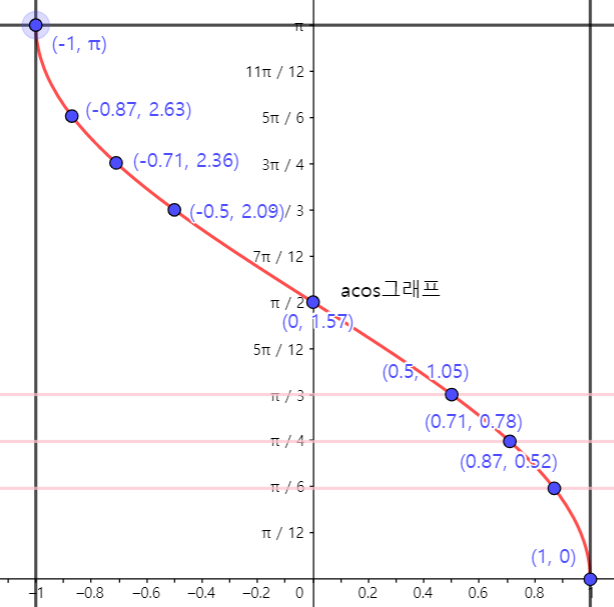
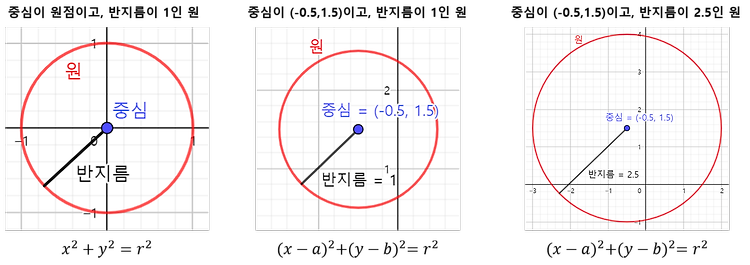
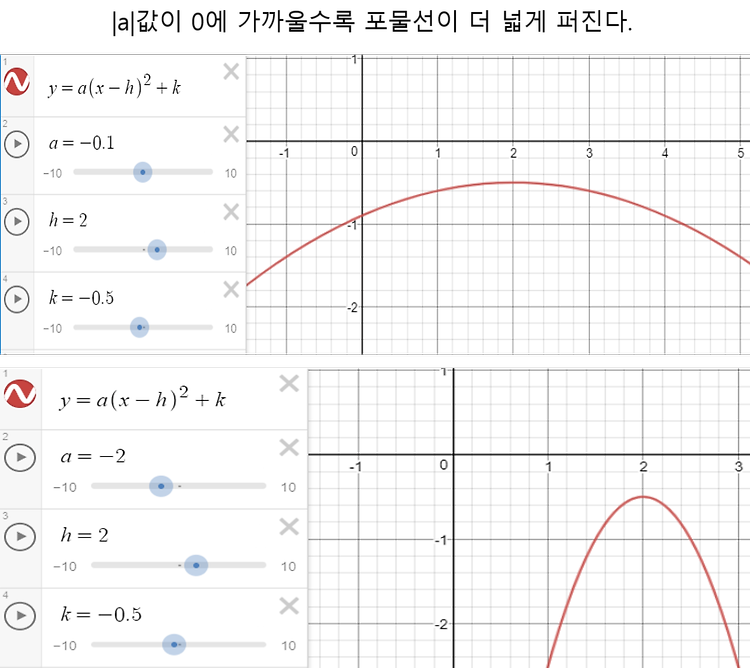
정의에서 나오는 항등식 # tanX = sinX/cosX, cotX = cosX/sinX = 1/tanX, cscX = 1/sinX, secX = 1/cosX 주기성에서 나오는 항등식 # sinθ = sin(X+2kπ), cosθ = cos(X+2kπ), tanθ = tan(X+2kπ), secθ = sec(X+2kπ), cscθ = csc(X+2kπ), cotθ = cot(X+2kπ) # θ가 360도(2π)를 넘으면 θ 대신 θ를 360도(2π)로 나눈 나머지(=X)를 넣어도 같은 값이 나온다는 뜻 # 이는 그래프를 보면 쉽게 확인할 수 있다. 대칭성에서 나오는 항등식 //부호 주의 # 음수각 바꾸기 : sin(-X) = -sinX, cos(-X) = cosX, tan(-X) = -tanX, csc(..

삼각함수의 그래프 삼각함수의 그래프 (기본) y = sin(θ) y = cos(θ) y = tan(θ) y = csc(θ) y = sec(θ) y = cot(θ) y = asin(θ) y = acos(θ) y = acot(θ) 삼각함수의 그래프의 주기 조절 # sin함수로만 그래프를 그렸다. cos도 똑같고, 나머지에는 의미가 없다. y = sin(θ) y = sin(θ/2) y = sin(2θ) 삼각함수의 그래프의 범위 조절 # 예시로 찍어놓은 점의 값이 잘못 나와있으니 주의 y = sin(θ) y = 2*sin(θ) y = 1/2*sin(θ) 삼각함수 그래프의 기준점 변경. y = sin(θ) y = sin(θ+aπ) - b (원점에 있던 기준점이 (aπ,b)로 이동함

각도의 표현 : degree vs radian # 주로 n˚(n도)로 표시하는 degree각은 원의 각도를 360도로 나누는 60분법에서 쓰이는 각도이다. # 주로 nπ로 표시하는 라디안각은 각을 호의 길이와 반지름의 비율로 나타내는 호도법에서 쓰이는 각도이다. # 특수각의 변환 degree 0˚ 30˚ 45˚ 60˚ 90˚ 120˚ 135˚ 150˚ 180˚ 270˚ 360˚ radian 0 1/6*π 1/4*π 1/3*π 1/2*π 2/3π 4/3*π 5/6*π π 3/2*π 2π # degree를 radian으로 변환 : n˚ * π/180˚ = nπ # radian을 degree로 변환 : nπ * 180˚/π = n˚ # 그런데 프로그래밍시에는 결국 파이값을 근사치의 상수로 정의해서 쓰기 때문에..

원 (Circle) # 원은 평면 위의 한 점으로부터 반지름만큼 떨어진 점들의 집합이다. # 중심이 (a,b)이고 반지름이 r인 원의 방정식은 (x-a)^2+(y-b)^2=r^2이다. # (기초적인) 원을 나타내는 구조체 struct circle { float center[2]; float radius; }; 구 (Sphere) # 구는 공간 위의 한 점으로부터 반지름만큼 떨어진 점들의 집합이다. # 중심이 (a,b,c)이고 반지름이 r인 구의 방정식은 (x-a)^2+(y-b)^2+(z-c)^2=r^2이다. struct sphere { float center[3]; float radius; }; 충돌 체크 # 원이나 구나 충돌체크 원리는 똑같다. # 두 원이나 구의 반지름의 합과 중심 간의 거리를 비교하..

포물선 # 포물선은 평면 위의 한 점F와 그 점을 지나지 않는 한 직선L까지의 거리가 같은 점들의 집합이다. # 점F를 포물선의 초점, 직선L을 포물선의 준선, 초점을 지나고 준선과 직교하는 직선을 축, 축과 포물선이 만나는 점을 꼭짓점이라고 한다. # 초점과 준선에 대한 내용은 고교수학을 정리할 때 다루기로 하자. # 포물선은 주로 투사체의 운동을 모델링하는데 쓰인다. # 꼭지점이 원점이면 그래프의 형태가 단순하다. # 그래프가 y=ax^2꼴이면 포물선은 y축에 대칭이고, x=ay^2 x축에 대칭이다. # 그래프가 y축에 대칭일때, a>0이면 위쪽으로 열려있고 (꼭지점이 y 최소값), a0이면 오른쪽으로 열려있고 (꼭지점이 x 최소값), a

피타고라스의 정리 # 피타고라스의 정리는 직각삼각형의 세 변 사이의 길이에 대한 정리이다. # 이를 이용하면 두 점 사이의 거리를 알 수 있다. # 또한 두 점 p1{x1,y1}, p2{x2,y2} 사이의 중점을 M이라 하면 M은 {(x1+x2)/2, (y1+y2)/2}이다. # 만약 두 점이 공간상의 점이라면 중점 M은 {(x1+x2)/2, (y1+y2)/2, (z1+z2)/2}로 구할 수 있다. # 이를 확장하면 공간도형의 중심점을 구하는 식을 만들 수 있다. # 평면 도형에서는 z축을 빼면 된다.

2D 공간에서 직선 표현하기 1. 직교 좌표계 : 2차원 직교 좌표계의 방정식을 대수적 방정식이라 한다. # 기본적인 직선의 (대수적) 방정식들 # 직선의 방정식의 일반형 : ax + by + c = 0, 표준형 : y = ax + b # 기울기가 m, y절편이 n인 직선의 방정식 : y = mx + n # 기울기가 m, 점(a,b)를 지나는 직선의 방정식 : y-b = m(x-a) -> y = mx + (b-ma) # 점(a,b)와 점(c,d)를 지나는 직선의 방정식 : [a!=c] (y-b) = ((d-b)/(c-a)) * (x-a), [a==c] x = a # 점(a,b)를 지나고 x축에 평행한 직선의 방정식 : y = b # 점(a,b)를 지나고 y축에 평행한 직선의 방정식 : x = a # x절..

2D에서의 좌표계 a) 직교 좌표계 / b) 구 좌표계 a-1) 데카르트 좌표계 / a-2) 화면 좌표계 1. 데카르트 좌표계 (혹은 Cartesian Coordinate System) # x축의 양의 방향이 오른쪽을 향하고, y축의 양의 방향이 윗쪽을 향하는 좌표계. # 일반적인 2D 수학에서 쓰이는 좌표계 # x축과 y축이 직교하는 직교 좌표계이다. # 2D 직교 좌표계의 점은 일반적으로 (x, y)로 표현한다. 2. 화면 좌표계 # x축의 양의 방향이 오른쪽을 향하고, y축의 양의 방향이 아래쪽을 향하는 죄표계. # 컴퓨터 화면은 위에서 아래로 읽으므로 y축의 양의 방향이 아래를 향한다. # 기본적으로 픽셀 단위를 사용하며 화면의 좌측 상단이 0,0이 된다. # x축과 y축이 직교하는 직교 좌표계이..

목차 # '게임 프로그래머를 위한 기초 수학과 물리'의 수학 파트를 기준으로 한다. 1장. 점과 직선 : 점과 선을 2D와 3D에서 정의하고, 충돌 검출에 대하여 다룬다. 1) 점을 정의하기 2) 직선을 정의하기 3) 직선의 성질 4) 충돌 검출에의 응용 2장. 기하학적 기초 : 피타고라스의 정리와 거리 공식, 중점 공식을 소개하고, 원, 포물선, 구 등의 기하학적 도형의 방정식을 정리한다. 1) 두 점 사이의 거리 2) 포물선 3) 원과 구 4) 충돌 검출에의 응용 3장. 삼각함수의 기초 : 6개의 삼각함수를 속성과 함께 정의하고, C++ 수학함수의 사용법과 라디안 각도 체계를 소개한다. 1) 각도 vs 라디안 2) 삼각함수 3) 삼각함수 항등식 4장. 벡터 연산 : 각종 벡터 형식을 소개하고, 벡터합..