UpWrite

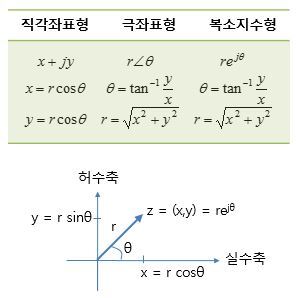
1. 허수단위와 복소수의 뜻 # 허수단위 : 제곱해서 -1이 되는 수를 문자 i 로 나타내어 i2 = -1이라 정하고 i 를 허수 단위라 한다. # 복소수 : a, b가 실수일 때 a+b*i 꼴의 수를 복소수라 하고 이 때, a를 실수 부분, b를 허수 부분이라 한다. 2. 복소수가 서로 같을 조건 # a,b,c,d가 서로 실수일 때, a+b*i = c+d*i ⇔ a = c, b = d // a+b*i = 0 ⇔ a = 0, b = 0 # 허수 부가 있는 복소수끼리는 대소 비교를 할 수 없다. 2-1. 무리수가 서로 같을 조건 # a,b,c,d가 서로 실수일 때, a+b√x = c+d√x ⇔ a = c, b = d // a+b√x = 0 ⇔ a = 0, b = 0 3. 복소수의 덧셈과 뺄셈 # 두 복소수..

// 구현 예시임 header struct float2x2 { union { struct { float _11, _12; float _21, _22; }; float m[2][2]; float2 _1, _2; }; float2x2(); float2x2(float2 __1, float2 __2); //복사연산자 기본값으로 정의 float2x2(const float2x2&) = default; float2x2(float2x2&&) = default; //대입연산자 기본값으로 정의 float2x2& operator= (const float2x2&) = default; float2x2& operator= (float2x2&&) = default; }; struct float3x3 { union { struct ..

// 그냥 "이런식으로 구현할 수 있다." 의 수준이므로 실제 사용은 상용 라이브러리를 쓸 것을 권장. DirectXMath.h라던가... xnamath.h라던가...// 그러므로 include문은 생략. header struct float2 { union { struct { float x, y; }; float f[2]; }; float2(); float2(float _x, float _y); }; struct Vector2 : float2 { static const Vector2 Zero2; static const Vector2 UnitX2; static const Vector2 UnitY2; //생성자 Vector2(); explicit Vector2(float x); Vector2(float x,..

단위행렬(Identity Matrix) # [A]가 정방행렬이고, i=j일 때, aij가 1이면 [A]를 단위행렬이라 한다. 기호로는 E나 I로 표시한다. (본 블로그에서는 단위행렬을 [1]로 표시한다.) # 나머지는 그냥 위의 이미지로 확인하자. 지금으로서는 중요하지 않다. # [1]*[A] = [A]*[1] = [A]. // 즉, 단위행렬은 행렬의 곱셈에 대한 항등원이다. 역행렬(Inverse Matrix) # 일단 [A]의 역행렬을 [A]-1로 표시하기로 하자. # [A] * [B] = [1] 일 때 [B] = [A]-1이다. 즉 [A]-1은 곱셈에 대한 [A]의 역원이다. # 역행렬을 계산하는 것은 꽤나 까다로운 문제이다. // 밑에서 다룬다. 전치행렬(Transposed Matrix) # [A]..

행렬의 기본 # 행렬 : 상수나 변수를 직사각형 꼴로 배열한 것. # 성분 : 행렬을 이루는 각각의 상수나 변수. # 행 : 성분의 가로 배열, # 열 : 성분의 세로 배열 # m*n행렬 : m개의 행과 n개의 열로 이루어진 행렬 # n차 정사각행렬 혹은 n차 정방행렬 : 행과 열이 n개로 서로 같은 행렬. # (i,j)성분 혹은 aij : 행렬의 i행, j열 성분을 (i,j)성분이라 하고 대체로 A행렬이면 성분을 aij로 표현한다. # 행렬 A를 간단히 A = (aij)로 나타내기도 한다. # 행렬의 행과 열 갯수가 서로 같고, 같은 위치의 성분이 모두 같으면 서로 같은 행렬이라 한다. # 행벡터 : 행이 한개뿐인 벡터, # 열벡터 : 열이 한개뿐인 벡터 행렬의 연산 (1) : 실수배와 덧셈 (앞으로 ..

0. 명제의 정의 # 명제는 기본적으로 "누구에게나 동일한 진리치를 갖는 문장"이라고 정의할 수 있다. # 하지만 명제를 더 엄밀하게 정의하고 논의할 필요가 있는 분야에서 엄밀하게 정의하는 것과 간단하게 정의하는 것은 조금 다르다. # 고교수학에서는 명제를 "가치판단이 개입될 수 없는, 누구나 참인지 거짓인지 일치된 판단을 할 수 있는 문장"이라고 간단하게 소개한다. # 하지만 위의 정의는 대표적으로 아래와 같은 문제를 갖는다. 1) 수학적 혹은 논리적으로 같은 의미를 갖어도 언어가 다르면 다른 문장이 되므로 명제를 문장이라고 하기에는 문제가 있다. 2) 직관적으로는 명제지만 인류가 아직 참인지 거짓인지 알 수 없는 문장이 있고, 그런 문장에 대해서는 '일치된 판단'이 불가능하다. 3) 직관적으로 명제이..

0. 직관적 집합론과 공리적 집합론 # 기본적으로 고교과정에서 배우는 집합개념은 직관적 집합론으로 집합을 직관적으로 받아들인다. # 공리적 집합론은 집합을 수학적으로 엄밀하게 정의하는 학문으로 수학과 학부 또는 대학원 과정에서 배우게 된다. # 집합을 수학적으로 엄밀하게 정의하는 이유는 집합을 그저 '어떠한 조건을 만족하는 것들의 모임'으로 정의하면 러셀의 역설 등에 의해 수학구조가 붕괴되기 때문이다. # 그래서 러셀의 역설 이후 현대 수학의 기초는 공리적 집합론을 기반으로 형성되었다. 현대수학에서 표준적으로 사용하는 공리계는 ZFC공리계이다. # 그러므로 고교 수학에서는 집합을 직관적으로 받아들이긴 하지만 정확하게 공부하기 위해서는 엄밀한 집합 개념이 필요하다. 1. 기본. # 집합의 정의 : 어떠한 ..

벡터와 사원수 # 벡터는 사실 사원수를 이용한 공간 표현을 더 쉽고 일반적으로 바뀌기 위해서 등장한 개념이다. # 그래서 벡터의 곱셈인 내적과 외적은 결국 사원수의 곱셈으로부터 기원했다고 볼 수 있다. # 게다가 외적은 사원수로부터 그냥 정의된 것도 아니다. # 즉, 내적과 외적에 대해서 제대로 이해하려면 사원수로부터 출발해야한다는 뜻이다. # 그래서 외적은 기본적으로 3차원 평면에서만 정의한다. (8원수로 7차원이나, 16원수로 15차원에서도 정의할 수는 있지만 의미가 없다) # 사원수를 처음 정립한 해밀턴은 실수부를 스칼라부, 허수부를 벡터부라 했다. # 그래서 사원수의 벡터와 구분하기 위해서 일반적인 벡터를 '좌표계 기반 벡터'라고 한다. # 즉, 실수부가 0인 사원수 두개의 곱을 벡터와 벡터의 곱..

내적과 외적 # 내적과 외적은 벡터끼리의 곱셈이라고 볼 수 있다. # 하지만 내적이나 외적이나 역원을 정의할 수 없기 때문에 벡터끼리의 나눗셈은 정의되어 있지 않다. + 추가 : 나눗셈을 정의할 수 없는 건 우리가 지금 좌표계 기반 벡터를 다루고 있기 때문이다. 벡터의 연산(2) : 내적 혹은 스칼라곱 # 원래 내적은 두 벡터 사이에 점을 찍는데 마땅한게 없으므로 ●을 내적을 나타내는 기호로 사용했다. # 벡터의 내적은 결과가 스칼라값으로 나온다. 그래서 내적을 스칼라곱이라고도 한다. # 그러므로 ●●와 같이 연속해서 내적하는 것은 불가능하다. # 내적은 두 벡터의 크기를 서로 곱하는 것이다. # 이를 이해하기위해 벡터가 아니라 두개의 1차원의 스칼라 값의 곱을 생각해보자. (결국 그냥 한개의 숫자다.)..

벡터와 스칼라 : 정의 # 스칼라 : 크기만 갖는 값 (ex : 질량, 속력, 에너지, 학생수 등) # 벡터 : 크기와 함께 방향을 갖는 값 (ex : 무게, 속도, 변위, 힘 등) 벡터의 표현 # = 벡터 a (이 블로그에서만 사용할 벡터표기법임) # 다렉은 기본적으로 벡터를 행벡터로 저장하고, OpenGL 등은 열벡터로 저장한다. # 프로그래밍에서는 결국 직교좌표계를 쓴다.# 구면좌표계에서의 표현은 그 벡터가 포함된 평면을 극좌표계라 생각해서 나타내는 방식이라 생각하면 된다. 벡터의 좌표계 변환 # 극좌표계 => 직교좌표계 : 극좌표 벡터가 ||A||@B이면 직교좌표 벡터 ai+bj는 a = ||A||cosB, b는 ||A||sinB # 직교좌표계 => 극좌표계 : 직교좌표 벡터가 ai+bj이면 극좌..