UpWrite

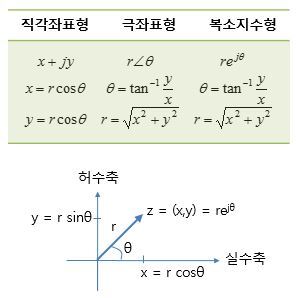
수학 공부 카테고리 목록 아래 카테고리는 "게임 프로그래머를 위한 기초 수학과 물리 (제우미디어, 2007)" 라는 책의 수학 파트를 기준으로 정리한 것이다. 고교 수학 부분은 더 정리해야하지만 일단 작성한 부분만 정리해두었다. 게임 프로그래머를 위한 기초 수학과 물리 기준 1. 기본 개요 2. 좌표계 정의와 점의 표현 3. 직선의 방정식 (2D 공간에서) 4. 두 점 사이의 거리와 중점 구하기 5. 포물선 6. 원과 구 7. 삼각함수 (1) - 정의와 기하학적 의미 8. 삼각함수 (2) - 삼각함수의 그래프 9. 삼각함수(3) - 삼각함수 항등식 10. 벡터(1) - 벡터의 정의와 기본연산 11. 벡터(2) - 내적 12. 벡터(3) - 외적 13. 행렬(1) -행렬의 정의와 연산 14. 행렬(2) -..

문제 해답 L 목표 달성 E 목표 달성 풀이 L 목표 풀이 1. 직선AB에 대한 수직이등분선을 긋는다. - 직선AB위에 점E가 생겼다. 2. 직선CD에 대한 수직이등분선을 긋는다. - 직선CD위에 점F가 생겼다. 3. 선분EF를 긋는다. E 목표 해설 1. 직선AD를 긋는다. 2. 직선BC를 긋는다. - 직선AD와 BC의 교점E가 생겼다. 3. 직선AC를 긋는다. 4. 직선BD를 긋는다. - 직선AC와 BD의 교점F가 생겼다. 5. 직선EF를 긋는다. 해설 # L목표는 증명이 필요 없으므로 생략. # 하지만 E목표는 증명이 어렵다. 일단 자료만 첨부 : 사다리꼴의 성질 참고자료 # 사다리꼴의 성질 1. 빗변을 기준으로 이웃한 두 각은 서로 보각관계이다. 즉, 두 각의 합이 180도. 2. 사다리꼴의 넓이..

문제 힌트 1. 원과 한 점에서 접하는 직선을 원의 접선이라고 한다. 2. 원의 접선은 원과 한 점에서 만나고 원의 반지름과 직교한다. 3. 원의 접선에서 원의 중심으로 올린 수선은 반지름과 크기가 같다. 해답 L목표 달성 E목표 달성 풀이 L목표 풀이 1. 점A,B가 만드는 직선AB의 수직이등분선을 긋는다. 2. 주어진 직선과 점B를 중심으로 하는 각의 이등분선을 긋는다. - 1에서 그은 직선과 2에서 지은 직선의 교점G가 생겼다. 3. 점G를 중심으로 하고 선분BG를 반지름으로 하는 원G를 그린다. E목표 풀이 1. 점A를 중심으로 하고, 선분AB를 반지름으로 하는 원A를 그린다. - 원A와 주어진 선분의 교점 E가 생겼다. 2. 점B를 중심으로 하고, 선분BA를 반지름으로 하는 원B를 그린다. - ..

1. 허수단위와 복소수의 뜻 # 허수단위 : 제곱해서 -1이 되는 수를 문자 i 로 나타내어 i2 = -1이라 정하고 i 를 허수 단위라 한다. # 복소수 : a, b가 실수일 때 a+b*i 꼴의 수를 복소수라 하고 이 때, a를 실수 부분, b를 허수 부분이라 한다. 2. 복소수가 서로 같을 조건 # a,b,c,d가 서로 실수일 때, a+b*i = c+d*i ⇔ a = c, b = d // a+b*i = 0 ⇔ a = 0, b = 0 # 허수 부가 있는 복소수끼리는 대소 비교를 할 수 없다. 2-1. 무리수가 서로 같을 조건 # a,b,c,d가 서로 실수일 때, a+b√x = c+d√x ⇔ a = c, b = d // a+b√x = 0 ⇔ a = 0, b = 0 3. 복소수의 덧셈과 뺄셈 # 두 복소수..

문제 해답LE목표 달성 E목표 달성 - 자와 컴파스만을 이용한 작도 V목표 달성 풀이 LEV목표 풀이 1. 선분AM의 수직이등분선을 긋는다. - 각BAC와 수직이등분선의 교점 D와 F가 생겼다. 2. 점M을 중심으로 하고 선분DM을 반지름으로 하는 원M을 그린다. 3. 선분DM을 그린다. 4. 선분ME를 그린다. 5. 선분MF를 그린다. EV목표 풀이 - 자와 컴퍼스만을 이용한 작도 1. 점A를 중심으로 하고 선분AM를 반지름으로 하는 원A를 그린다. 2. 점M를 중심으로 하고 선분MA를 반지름으로 하는 원M를 그린다. - 원A와 M의 교점 D와 E가 생겼다. 3. 선분DE를 긋는다. - 선분DE와 각A의 교점 F가 생겼다. 4. 점M을 중심으로 하고 선분MF를 반지름으로 하는 원M을 그린다. - 원M과..

문제 힌트 해답 L, E목표 동시 달성 풀이 1. 점D를 중심으로 하고 선분AD를 반지름으로 하는 원D를 그린다. - 원D와 각A에 대한 교점E,F가 생겼다. 2. 선분EF를 그린다. 해설 # 점O가 삼각형의 각변의 수직이등분선의 교점이라는 뜻은 점O가 삼각형의 외심이라는 뜻이다. # 삼각형의 외심은 삼각형의 외접원의 중점이다. # 또한 삼각형의 각 꼭짓점에서 외심까지의 길이는 외접원의 반지름과 일치하므로 같다. # 위 그림의 초록색 직선ID, DJ, DH는 지오지브라로 그린 삼각형의 각 변의 수직이등분선이다.참고자료 외심의 위치 직각삼각형의 외심은 빗변의 중심에 위치한다. 둔각삼각형의 외심은 삼각형 바깥에 위치한다. 예각삼각형의 외심은 삼각형의 내부에 위치한다.

문제 해답L목표 달성 E목표 달성 풀이L목표 풀이 1. 반직선AG와 점D를 잇는 수선을 그린다. - 수선과 반직선AH를 잇는 교점F가 생겼다. 2. 반직선AH와 점D를 잇는 수선을 그린다. - 수선과 반직선AG를 잇는 교점E가 생겼다. 3. 선분EF를 긋는다. E목표 풀이 1. 점A를 중심으로 하고 선분AD를 반지름으로 하는 원A를 그린다. 2. 반직선AM위의 임의의 한 점E를 중심으로 하고 선분ED를 반지름으로 하는 원E를 그린다.- 원A와 원E의 교점F가 생겼다. 3. 반직선AN위의 임의의 한 점G를 중심으로 하고 선분GD를 반지름으로 하는 원G를 그린다.- 원A와 원G의 교점H가 생겼다. 4. 직선FD를 긋는다. - 반직선AN과 직선FD의 교점J가 생겼다. 5. 직선HD를 긋는다. - 반직선AM과 ..

문제 해답 L,E목표 동시 달성 L목표 달성 E목표 달성 풀이 L,E목표 풀이 1. 직선AC를 긋는다. 2. 선분AC의 수직인 선을 점C에서 긋는다. L목표 풀이 1. 직선AC를 긋는다. 2. 각DCA의 이등분선을 긋는다. E목표 풀이 1. 직선AC를 긋는다. 2. 원A 안의 임의의 점D를 중심으로 하고 선분DC를 반지름으로 하는 원D를 그린다. - 선분AC와 원D의 교점 F가 생겼다. 3. 직선FD를 긋는다. - 직선FD와 원D의 교점 G가 생겼다. 4. 직선CG를 긋는다. 해설 # LE목표 해설 : 생략 # L목표 해설 : 생략 # E목표 해설 1. 점C에서 선분CA에 대한 수선을 올린 것. 2. 2-7 공략 참고

문제 힌트 1. 마름모는 네변의 길이가 모두 같은 사각형이다. 2. 마름모의 두 대각선은 서로를 수직이등분한다. 1-2공략 참고 해답 L목표 E목표 동시달성 자와 컴퍼스만을 이용한 작도 풀이 L목표 E목표 풀이 1. 선분AC를 긋는다. 2. 선분BD를 긋는다. - 선분AC와 BD의 교점E를 찍는다. 3. 선분AB와 점E를 잇는 수선을 긋는다. - 선분AB와 수선의 교점F가 생겼다. 4. 점E를 중심으로 하고 선분EF를 반지름으로 하는 원E를 그린다. 자와 컴퍼스만을 이용한 작도 풀이 1. 선분AC를 긋는다. 2. 선분BD를 긋는다. - 선분AC와 BD의 교점E를 찍는다. 3. 점E를 중심으로 하고 선분AE를 반지름으로 하는 원E를 그린다. - 원E와 선분AD의 교점F가 생겼다. 4. 점A를 중심으로 하고..

문제 해답 L목표 달성 E목표 달성 풀이 L목표 풀이 1. 직선A에서 주어진 점C에 대한 수선을 그린다. - 직선A와 C의 교점D가 생겼다. 2. 점C를 중심으로 하고 선분CD를 반지름으로 하는 원C를 그린다.E목표 해설 1. 직선A 위의 임의의 점D를 중심으로 하고 선분CD를 반지름으로 하는 원D를 그린다. 2. 직선A 위의 임의의 점E를 중심으로 하고 선분ED를 반지름으로 하는 원E를 그린다. - 원D와 E의 교점C와 F가 생겼다. 3. 점C와 F를 잇는 직선CF를 긋는다. - 직선A와 직선CF의 교점G가 생겼다. 4. 점C를 중심으로 하고 선분CG를 반지름으로 하는 원C를 그린다. 해설 L목표 해설 : 생략E목표 해설 # 직선A에서 C로 수선을 올린다. (2-6공략의 E목표 해설 참조) # 직선A와..