UpWrite

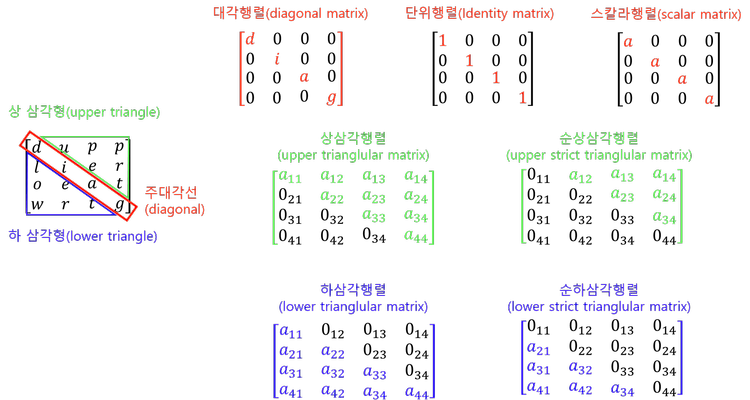
단위행렬(Identity Matrix) # [A]가 정방행렬이고, i=j일 때, aij가 1이면 [A]를 단위행렬이라 한다. 기호로는 E나 I로 표시한다. (본 블로그에서는 단위행렬을 [1]로 표시한다.) # 나머지는 그냥 위의 이미지로 확인하자. 지금으로서는 중요하지 않다. # [1]*[A] = [A]*[1] = [A]. // 즉, 단위행렬은 행렬의 곱셈에 대한 항등원이다. 역행렬(Inverse Matrix) # 일단 [A]의 역행렬을 [A]-1로 표시하기로 하자. # [A] * [B] = [1] 일 때 [B] = [A]-1이다. 즉 [A]-1은 곱셈에 대한 [A]의 역원이다. # 역행렬을 계산하는 것은 꽤나 까다로운 문제이다. // 밑에서 다룬다. 전치행렬(Transposed Matrix) # [A]..

행렬의 기본 # 행렬 : 상수나 변수를 직사각형 꼴로 배열한 것. # 성분 : 행렬을 이루는 각각의 상수나 변수. # 행 : 성분의 가로 배열, # 열 : 성분의 세로 배열 # m*n행렬 : m개의 행과 n개의 열로 이루어진 행렬 # n차 정사각행렬 혹은 n차 정방행렬 : 행과 열이 n개로 서로 같은 행렬. # (i,j)성분 혹은 aij : 행렬의 i행, j열 성분을 (i,j)성분이라 하고 대체로 A행렬이면 성분을 aij로 표현한다. # 행렬 A를 간단히 A = (aij)로 나타내기도 한다. # 행렬의 행과 열 갯수가 서로 같고, 같은 위치의 성분이 모두 같으면 서로 같은 행렬이라 한다. # 행벡터 : 행이 한개뿐인 벡터, # 열벡터 : 열이 한개뿐인 벡터 행렬의 연산 (1) : 실수배와 덧셈 (앞으로 ..

문제 힌트 1. 평행사변형의 두 대각선은 서로를 수직이등분한다. 2. 평행사변형의 중점에서 각 꼭지점까지의 거리는 모두 같다. 해답 L목표 달성 E목표 달성 풀이 L목표 1. 점B와 점A를 잇는 직선을 긋는다. 2. 점B와 직선BA와 원A의 교점C에 대한 수직이등분선을 긋는다. 3. 원A 위의 점 4개(B,C,D,E)를 이어서 사각형을 만든다. E목표 1. 점B를 중심으로 하고 BA를 반지름으로 하는 원을 그린다. -> 원A와 원B의 교점C와 D가 생겼다. 2. 점C를 중심으로 하고 CD를 반지름으로 하는 원을 그린다. (반대로 해도 상관없다.) -> 원A와 원C의 교점E가 추가로 생겼다. 3. 점A와 점C를 잇는 직선을 긋는다. -> 직선AC와 원C가 만나는 교점 F와 G가 생겼다. 4. 점F와 점E를..

0. 직관적 집합론과 공리적 집합론 # 기본적으로 고교과정에서 배우는 집합개념은 직관적 집합론으로 집합을 직관적으로 받아들인다. # 공리적 집합론은 집합을 수학적으로 엄밀하게 정의하는 학문으로 수학과 학부 또는 대학원 과정에서 배우게 된다. # 집합을 수학적으로 엄밀하게 정의하는 이유는 집합을 그저 '어떠한 조건을 만족하는 것들의 모임'으로 정의하면 러셀의 역설 등에 의해 수학구조가 붕괴되기 때문이다. # 그래서 러셀의 역설 이후 현대 수학의 기초는 공리적 집합론을 기반으로 형성되었다. 현대수학에서 표준적으로 사용하는 공리계는 ZFC공리계이다. # 그러므로 고교 수학에서는 집합을 직관적으로 받아들이긴 하지만 정확하게 공부하기 위해서는 엄밀한 집합 개념이 필요하다. 1. 기본. # 집합의 정의 : 어떠한 ..

지오지브라 수학 그래프 게산기. 2차원 그래프, 3차원 그래프 뿐만 아니라 기하학적 표현이나 확률계산까지 다 제공하는 만능 웹사이트.

벡터와 사원수 # 벡터는 사실 사원수를 이용한 공간 표현을 더 쉽고 일반적으로 바뀌기 위해서 등장한 개념이다. # 그래서 벡터의 곱셈인 내적과 외적은 결국 사원수의 곱셈으로부터 기원했다고 볼 수 있다. # 게다가 외적은 사원수로부터 그냥 정의된 것도 아니다. # 즉, 내적과 외적에 대해서 제대로 이해하려면 사원수로부터 출발해야한다는 뜻이다. # 그래서 외적은 기본적으로 3차원 평면에서만 정의한다. (8원수로 7차원이나, 16원수로 15차원에서도 정의할 수는 있지만 의미가 없다) # 사원수를 처음 정립한 해밀턴은 실수부를 스칼라부, 허수부를 벡터부라 했다. # 그래서 사원수의 벡터와 구분하기 위해서 일반적인 벡터를 '좌표계 기반 벡터'라고 한다. # 즉, 실수부가 0인 사원수 두개의 곱을 벡터와 벡터의 곱..

내적과 외적 # 내적과 외적은 벡터끼리의 곱셈이라고 볼 수 있다. # 하지만 내적이나 외적이나 역원을 정의할 수 없기 때문에 벡터끼리의 나눗셈은 정의되어 있지 않다. + 추가 : 나눗셈을 정의할 수 없는 건 우리가 지금 좌표계 기반 벡터를 다루고 있기 때문이다. 벡터의 연산(2) : 내적 혹은 스칼라곱 # 원래 내적은 두 벡터 사이에 점을 찍는데 마땅한게 없으므로 ●을 내적을 나타내는 기호로 사용했다. # 벡터의 내적은 결과가 스칼라값으로 나온다. 그래서 내적을 스칼라곱이라고도 한다. # 그러므로 ●●와 같이 연속해서 내적하는 것은 불가능하다. # 내적은 두 벡터의 크기를 서로 곱하는 것이다. # 이를 이해하기위해 벡터가 아니라 두개의 1차원의 스칼라 값의 곱을 생각해보자. (결국 그냥 한개의 숫자다.)..

벡터와 스칼라 : 정의 # 스칼라 : 크기만 갖는 값 (ex : 질량, 속력, 에너지, 학생수 등) # 벡터 : 크기와 함께 방향을 갖는 값 (ex : 무게, 속도, 변위, 힘 등) 벡터의 표현 # = 벡터 a (이 블로그에서만 사용할 벡터표기법임) # 다렉은 기본적으로 벡터를 행벡터로 저장하고, OpenGL 등은 열벡터로 저장한다. # 프로그래밍에서는 결국 직교좌표계를 쓴다.# 구면좌표계에서의 표현은 그 벡터가 포함된 평면을 극좌표계라 생각해서 나타내는 방식이라 생각하면 된다. 벡터의 좌표계 변환 # 극좌표계 => 직교좌표계 : 극좌표 벡터가 ||A||@B이면 직교좌표 벡터 ai+bj는 a = ||A||cosB, b는 ||A||sinB # 직교좌표계 => 극좌표계 : 직교좌표 벡터가 ai+bj이면 극좌..

정의에서 나오는 항등식 # tanX = sinX/cosX, cotX = cosX/sinX = 1/tanX, cscX = 1/sinX, secX = 1/cosX 주기성에서 나오는 항등식 # sinθ = sin(X+2kπ), cosθ = cos(X+2kπ), tanθ = tan(X+2kπ), secθ = sec(X+2kπ), cscθ = csc(X+2kπ), cotθ = cot(X+2kπ) # θ가 360도(2π)를 넘으면 θ 대신 θ를 360도(2π)로 나눈 나머지(=X)를 넣어도 같은 값이 나온다는 뜻 # 이는 그래프를 보면 쉽게 확인할 수 있다. 대칭성에서 나오는 항등식 //부호 주의 # 음수각 바꾸기 : sin(-X) = -sinX, cos(-X) = cosX, tan(-X) = -tanX, csc(..

삼각함수의 그래프 삼각함수의 그래프 (기본) y = sin(θ) y = cos(θ) y = tan(θ) y = csc(θ) y = sec(θ) y = cot(θ) y = asin(θ) y = acos(θ) y = acot(θ) 삼각함수의 그래프의 주기 조절 # sin함수로만 그래프를 그렸다. cos도 똑같고, 나머지에는 의미가 없다. y = sin(θ) y = sin(θ/2) y = sin(2θ) 삼각함수의 그래프의 범위 조절 # 예시로 찍어놓은 점의 값이 잘못 나와있으니 주의 y = sin(θ) y = 2*sin(θ) y = 1/2*sin(θ) 삼각함수 그래프의 기준점 변경. y = sin(θ) y = sin(θ+aπ) - b (원점에 있던 기준점이 (aπ,b)로 이동함