UpWrite

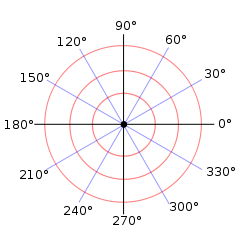
각도의 표현 : degree vs radian # 주로 n˚(n도)로 표시하는 degree각은 원의 각도를 360도로 나누는 60분법에서 쓰이는 각도이다. # 주로 nπ로 표시하는 라디안각은 각을 호의 길이와 반지름의 비율로 나타내는 호도법에서 쓰이는 각도이다. # 특수각의 변환 degree 0˚ 30˚ 45˚ 60˚ 90˚ 120˚ 135˚ 150˚ 180˚ 270˚ 360˚ radian 0 1/6*π 1/4*π 1/3*π 1/2*π 2/3π 4/3*π 5/6*π π 3/2*π 2π # degree를 radian으로 변환 : n˚ * π/180˚ = nπ # radian을 degree로 변환 : nπ * 180˚/π = n˚ # 그런데 프로그래밍시에는 결국 파이값을 근사치의 상수로 정의해서 쓰기 때문에..

원 (Circle) # 원은 평면 위의 한 점으로부터 반지름만큼 떨어진 점들의 집합이다. # 중심이 (a,b)이고 반지름이 r인 원의 방정식은 (x-a)^2+(y-b)^2=r^2이다. # (기초적인) 원을 나타내는 구조체 struct circle { float center[2]; float radius; }; 구 (Sphere) # 구는 공간 위의 한 점으로부터 반지름만큼 떨어진 점들의 집합이다. # 중심이 (a,b,c)이고 반지름이 r인 구의 방정식은 (x-a)^2+(y-b)^2+(z-c)^2=r^2이다. struct sphere { float center[3]; float radius; }; 충돌 체크 # 원이나 구나 충돌체크 원리는 똑같다. # 두 원이나 구의 반지름의 합과 중심 간의 거리를 비교하..

포물선 # 포물선은 평면 위의 한 점F와 그 점을 지나지 않는 한 직선L까지의 거리가 같은 점들의 집합이다. # 점F를 포물선의 초점, 직선L을 포물선의 준선, 초점을 지나고 준선과 직교하는 직선을 축, 축과 포물선이 만나는 점을 꼭짓점이라고 한다. # 초점과 준선에 대한 내용은 고교수학을 정리할 때 다루기로 하자. # 포물선은 주로 투사체의 운동을 모델링하는데 쓰인다. # 꼭지점이 원점이면 그래프의 형태가 단순하다. # 그래프가 y=ax^2꼴이면 포물선은 y축에 대칭이고, x=ay^2 x축에 대칭이다. # 그래프가 y축에 대칭일때, a>0이면 위쪽으로 열려있고 (꼭지점이 y 최소값), a0이면 오른쪽으로 열려있고 (꼭지점이 x 최소값), a

피타고라스의 정리 # 피타고라스의 정리는 직각삼각형의 세 변 사이의 길이에 대한 정리이다. # 이를 이용하면 두 점 사이의 거리를 알 수 있다. # 또한 두 점 p1{x1,y1}, p2{x2,y2} 사이의 중점을 M이라 하면 M은 {(x1+x2)/2, (y1+y2)/2}이다. # 만약 두 점이 공간상의 점이라면 중점 M은 {(x1+x2)/2, (y1+y2)/2, (z1+z2)/2}로 구할 수 있다. # 이를 확장하면 공간도형의 중심점을 구하는 식을 만들 수 있다. # 평면 도형에서는 z축을 빼면 된다.

2D 공간에서 직선 표현하기 1. 직교 좌표계 : 2차원 직교 좌표계의 방정식을 대수적 방정식이라 한다. # 기본적인 직선의 (대수적) 방정식들 # 직선의 방정식의 일반형 : ax + by + c = 0, 표준형 : y = ax + b # 기울기가 m, y절편이 n인 직선의 방정식 : y = mx + n # 기울기가 m, 점(a,b)를 지나는 직선의 방정식 : y-b = m(x-a) -> y = mx + (b-ma) # 점(a,b)와 점(c,d)를 지나는 직선의 방정식 : [a!=c] (y-b) = ((d-b)/(c-a)) * (x-a), [a==c] x = a # 점(a,b)를 지나고 x축에 평행한 직선의 방정식 : y = b # 점(a,b)를 지나고 y축에 평행한 직선의 방정식 : x = a # x절..

2D에서의 좌표계 a) 직교 좌표계 / b) 구 좌표계 a-1) 데카르트 좌표계 / a-2) 화면 좌표계 1. 데카르트 좌표계 (혹은 Cartesian Coordinate System) # x축의 양의 방향이 오른쪽을 향하고, y축의 양의 방향이 윗쪽을 향하는 좌표계. # 일반적인 2D 수학에서 쓰이는 좌표계 # x축과 y축이 직교하는 직교 좌표계이다. # 2D 직교 좌표계의 점은 일반적으로 (x, y)로 표현한다. 2. 화면 좌표계 # x축의 양의 방향이 오른쪽을 향하고, y축의 양의 방향이 아래쪽을 향하는 죄표계. # 컴퓨터 화면은 위에서 아래로 읽으므로 y축의 양의 방향이 아래를 향한다. # 기본적으로 픽셀 단위를 사용하며 화면의 좌측 상단이 0,0이 된다. # x축과 y축이 직교하는 직교 좌표계이..

목차 # '게임 프로그래머를 위한 기초 수학과 물리'의 수학 파트를 기준으로 한다. 1장. 점과 직선 : 점과 선을 2D와 3D에서 정의하고, 충돌 검출에 대하여 다룬다. 1) 점을 정의하기 2) 직선을 정의하기 3) 직선의 성질 4) 충돌 검출에의 응용 2장. 기하학적 기초 : 피타고라스의 정리와 거리 공식, 중점 공식을 소개하고, 원, 포물선, 구 등의 기하학적 도형의 방정식을 정리한다. 1) 두 점 사이의 거리 2) 포물선 3) 원과 구 4) 충돌 검출에의 응용 3장. 삼각함수의 기초 : 6개의 삼각함수를 속성과 함께 정의하고, C++ 수학함수의 사용법과 라디안 각도 체계를 소개한다. 1) 각도 vs 라디안 2) 삼각함수 3) 삼각함수 항등식 4장. 벡터 연산 : 각종 벡터 형식을 소개하고, 벡터합..

1) 거듭제곱과 거듭제곱근 1. 거듭제곱 ① 어떤 실수 a를 n번 곱한 것. ② \(a^n\)을 a의 n제곱이라고 읽는다. ③ 모든 n에 대한 \(a^n\)의 꼴을 a의 거듭제곱이라고 한다. ④ \(a^n\)에서 a를 밑, n을 지수라 한다. "어떤 수를 그 수로 여러번 곱하기."가 거듭 제곱이다. 예를 들어 \(2^5\) = 2*2*2*2*2 로 2를 5번 곱한 것을 의미하고, 값인 36은 \(2^5\)의 값이 된다. \(2^n\) 에서 n이 작으면 모를까 n이 큰 수이면 2*2*...*2 의 형태로 쓰기에는 너무 길어지니 줄인 것이다. 2. 거듭제곱근 ① a가 실수일 때, n제곱하여 a가 되는 수. ② \(x^n=a\)일 때, x를 a의 n제곱근이라고 한다. ③ 모든 n에 대한 \(x^n=a\) 꼴의..

항상 헷갈리는 행과열 행(row) : 가로방향 집합, 셀때는 세로 방향(위에서 아래로)으로 센다. 열(column) : 세로방향 집합, 셀때는 가로 방향(좌에서 우로)으로 센다. 일반적인 수학의 행렬은 a b c d e f g h i 가 있으면 a가 1행1열, b가 1행2열, c가 1행3열 d가 2행1열, e가 2행2열, f가 2행3열 g가 3행1열, h가 3행2열, i가 3행3열 일단 여기까지 참고 https://blog.naver.com/oranke/40000788158 [산수 02] 행기준 행렬과 열기준 행렬 뷰변환 행렬에 대해 살펴보기 전에 짚고 넘어가야 할 문제가 있습니다. OpenGL과 D3D를 말할 때... blog.naver.com

문제 힌트 외심 : 다각형의 외접원의 중심. (삼각형의 경우 세 변의 수직 이등분선의 교점과 같다) 해답 L목표 달성 E목표 달성 풀이 L목표 1. 점B와 점C의 수직이등분선을 긋는다. (두 점B와 C는 원A 위의 점이면 뭐든 상관없다.) 2. 점C와 점D의 수직이등분선을 긋는다. (점D도 원A 위의 점이면 어디든 상관없다) 3. 두 수직이등분선의 교점A를 찍는다. E목표 1. 원A 위의 점B를 중심으로 하는 원B를 그린다. (반지름은 원A와 B의 교점이 생길 정도로) - 원A와 B의 교점C가 생겼다. 2. 점C를 중점으로 하고 선분CB를 반지름으로 하는 원C를 그린다. - 원A와 원C의 교점D와 원B와 원C의 두 교점E와 F가 생겼다. 3. 직선EF를 긋는다. 4. 원D를 중심으로 하고 선분DC를 반지..