UpWrite

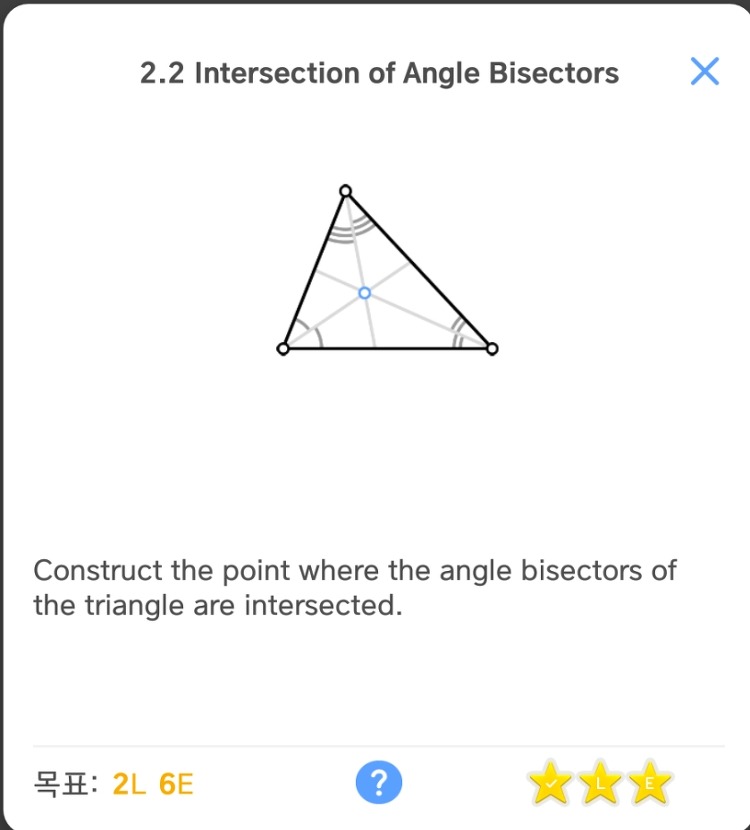
문제 힌트 해답 L목표 달성 E목표 달성 풀이 L목표 달성 1. 직선A 위의 임의의 점A와 주어진 점B, 직선A 위의 임의의 점C에 대한 각의 이등분선을 그린다. E목표 달성 1. 직선A 위에 있지 않은 임의의 점C를 중심으로 하고, 선분CB를 반지름으로 하는 원을 그린다. (점B는 주어진 점) - 직선A와 원C의 교점D가 생겼다. 2. 점D와 C를 이은 직선을 긋는다. - 직선CD와 원C의 교점E가 생겼다. 3. 점E와 점B를 이은 직선을 긋는다. 해설 L목표 해설 : 생략E목표 해설 1. 선분ED는 원C의 지름. 선분BD는 주어진 직선A와 점B를 포함하는 원C의 현. 2. 각ECD는 선분ED가 원의 지름이므로 180º ∴ 각EBD는 90º ∴ 삼각형EDB는 직각삼각형. 3. ∴ 직선EB와 직선A는 직..

문제 힌트 해답 L목표 달성 E목표 달성 풀이 L목표 달성 1. 주어진 점C를 중심으로 하는 원C를 직선A와 두개의 교점이 갖도록 그린다. - 원C와 직선A의 교점E와 F가 생겼다. 2. 선분EF에 대한 수직이등분선을 긋는다. E목표 달성 1. 직선A의 임의의 점D를 중심으로 하고 선분DC를 반지름으로 하는 원D를 그린다. 2. 직선A의 임의의 점E를 중심으로 하고 선분EC를 반지름으로 하는 원E를 그린다. - 원D와 E의 교점F가 생겼다. 3. 점C와 점F를 잇는 직선을 긋는다. 해설 L목표 해설 # 선분EF는 원C의 현이다. 그리고 직선GH는 현EF에 대한 수직이등분선이다. (도구의 정의) # 현의 수직이등분선은 원의 중심을 지난다. (현의 수직이등분선의 성질) 추가 해설 # 현의 수직이등분선의 성질..

문제 힌트 해답 풀이 1. 직선AC를 긋는다. 2. 직선BD를 긋는다. - 직선AC와 BD의 교점F가 생겼다. 3. 직선EF를 긋는다. 해설 # 점F는 사각형의 중점이다. 사각형의 중점과 사각형 밖의 한 점을 이은 직선은 사각형을 이등분한다. # 라지만 왜 그런지는 잘 모르겠으므로 합동인 도형들로 사각형 IDCJ와 AIJB의 넓이가 같음을 확인해보자. # 직선EF와 선분AD가 만나는 교점I와 직선EF와 선분BC가 만나는 교점J와 점I와 J에서 올린 수선의 발이 이루는 사각형KILJ에 의해 선분IF와 JF의 길이는 같다. (선분IJ가 사각형KILJ의 대각선이고, 점F는 원래 사각형의 중점이자 사각형KILJ의 중점이기도 하다.) # 삼각형ABF와 DCF는 SSS합동이다. (직사각형의 두 대각선은 서로를 이등..

문제 힌트 해답 L, E 목표 동시 달성 1 L, E 목표 동시 달성 2 V목표 달성1 풀이 L, E 목표 동시 달성 1 1. 점A를 중심으로 하는 원A를 그린다. -점A와 각A의 두 변과의 교점D, E가 생겼다. 2. 점D를 중심으로 하고 선분DE를 반지름으로 하는 원D를 그린다. - 원A와 D의 교점F가 생겼다. 3. 점A와 점E를 잇는 직선을 긋는다. L, E 목표 동시 달성 2 1. 각A의 한 변 위에 한점D를 중심으로 하고 선분DA를 반지름으로 하는 원D를 그린다. - 원D와 각A의 반대편 변과의 교점E가 생겼다. 2. 점A를 중심으로 하고 선분AE를 반지름으로 하는 원A를 그린다. - 원D와 원A의 교점F가 생겼다. 3. 점A와 점F를 잇는 직선을 긋는다.V 목표 달성 1 1. 점A를 중심으로..

문제 힌트 해답 L목표 달성 L,E목표 동시 달성 V목표 달성 풀이 L목표 달성 1. 반직선A의 임의의 위치에 점C를 잡고 점C를 중심으로 하고 선분 CA를 반지름으로 하는 원을 그린다. 2. 점A를 중심으로 하고 선분AC를 반지름으로 하는 원을 그린다. - 두 원의 교점D가 생겼다. 3. 각DAC를 이등분하는 이등분선을 그린다. LE목표 달성 1. 반직선A의 임의의 위치에 점C를 잡고 점C를 중심으로 하고 선분CA를 반지름으로 하는 원을 그린다. - 반직선 A와 원C가 만나는 교점D가 생겼다. 2. 점D를 중심으로 하고 선분DC를 반지름으로 하는 원D를 그린다. - 원C와 원D의 교점E가 생겼다. 3. 점A와 점E를 잇는 직선을 긋는다. V목표 달성 1. 반직선A의 임의의 위치에 점C를 잡고 점C를 중..

문제 2.2 각의 이등분선들의 교점 삼각형의 각의 이등분선들이 교차하는 점을 작도하세요. 해답 L목표 달성 E목표 달성 풀이 L목표 달성 1. 각BAC의 각이등분선을 긋는다. 2. 각ABC의 각이등분선을 긋는다. 3. 두 직선의 교점을 찍는다. E목표 달성 1. 점A를 중심으로 하고 선분AB를 반지름으로 하는 원A를 그린다. - 선분AC와 원A의 교점 E가 생겼다. 2. 점B를 중심으로 하고 선분BA를 반지름으로 하는 원B를 그린다. - 선분BC와 원B의 교점 D가 생겼다. 3. 점D를 중심으로 하고 선분BD를 반지름으로 하는 원D를 그린다. - 원A와 D의 교점 F가 생겼다. 4. 점B와 F를 잇는 직선을 긋는다. 5. 점E를 중심으로 하고 선분EA를 반지름으로 하는 원E를 그린다. - 원B와 E의 교..

문제 힌트 1. 두 변의 크기가 같은 삼각형을 이등변삼각형이라 한다. 이 때, 주로 다른 변과 같지 않은 한 변을 밑변이라고 한다. 2. 이등변 삼각형의 밑변의 양쪽 각의 크기는 같다. 3. 밑변의 대점에서 밑변으로 수선을 내리면 이 수선은 대점이 이루는 각과 밑변을 이등분한다. 해답 L목표, E목표 동시 달성 E목표 달성 풀이 L,E목표 동시 달성 1. 주어진 점A를 중심으로 하는 원을 하나 그린다. -> 원A와 각A의 두 반직선의 교점C,B가 생겼다. 2. 점C와 B의 수직이등분선을 긋는다. E목표 달성 1. 주어진 점A를 중심으로 하는 원을 하나 그린다. -> 원A와 각A의 두 반직선의 교점C,B가 생겼다. 2. 점B를 중심으로 하고 선분BA를 반지름으로 하는 원을 그린다. 3. 점C를 중심으로 하..

문제 힌트 1. 평행사변형의 두 대각선은 서로를 수직이등분한다. 2. 평행사변형의 중점에서 각 꼭지점까지의 거리는 모두 같다. 해답 L목표 달성 E목표 달성 풀이 L목표 1. 점B와 점A를 잇는 직선을 긋는다. 2. 점B와 직선BA와 원A의 교점C에 대한 수직이등분선을 긋는다. 3. 원A 위의 점 4개(B,C,D,E)를 이어서 사각형을 만든다. E목표 1. 점B를 중심으로 하고 BA를 반지름으로 하는 원을 그린다. -> 원A와 원B의 교점C와 D가 생겼다. 2. 점C를 중심으로 하고 CD를 반지름으로 하는 원을 그린다. (반대로 해도 상관없다.) -> 원A와 원C의 교점E가 추가로 생겼다. 3. 점A와 점C를 잇는 직선을 긋는다. -> 직선AC와 원C가 만나는 교점 F와 G가 생겼다. 4. 점F와 점E를..

문제 힌트 외심 : 다각형의 외접원의 중심. (삼각형의 경우 세 변의 수직 이등분선의 교점과 같다) 해답 L목표 달성 E목표 달성 풀이 L목표 1. 점B와 점C의 수직이등분선을 긋는다. (두 점B와 C는 원A 위의 점이면 뭐든 상관없다.) 2. 점C와 점D의 수직이등분선을 긋는다. (점D도 원A 위의 점이면 어디든 상관없다) 3. 두 수직이등분선의 교점A를 찍는다. E목표 1. 원A 위의 점B를 중심으로 하는 원B를 그린다. (반지름은 원A와 B의 교점이 생길 정도로) - 원A와 B의 교점C가 생겼다. 2. 점C를 중점으로 하고 선분CB를 반지름으로 하는 원C를 그린다. - 원A와 원C의 교점D와 원B와 원C의 두 교점E와 F가 생겼다. 3. 직선EF를 긋는다. 4. 원D를 중심으로 하고 선분DC를 반지..

문제 힌트 1. 마름모는 네변의 길이가 모두 같은 사각형이다. 2. 마름모의 두 대각선은 서로를 수직이등분한다. 1-2공략 참조 해답 L목표, V목표 달성 E목표 달성 풀이 L목표 1. 선분AC에 대한 수직이등분선을 그린다. - 선분AC에 대한 수직이등분선과 선분AB의 교점E와 선분DC의 교점G가 생겼다. 2. 사각형EBGD를 그린다.V목표 1. 선분BD에 대한 수직이등분선을 그린다. - 선분BD에 대한 수직이등분선과 선분AB의 교점F와 선분DC의 교점H가 생겼다. 2. 사각형AFCH를 그린다. E목표 1. 점A를 중심으로 하고 점C를 지나는 원A를 그린다. 2. 점C를 중심으로 하고 점A를 지나는 원C를 그린다. - 원A와 C의 교점E와 F가 생겼다. 3. 직선EF를 긋는다. - 직선EF와 선분BC의 ..